In 1991 we suggested a scientific idea
that early development of living organisms produces an exceptionally
high load of initial damage, which is comparable with the amount of
subsequent aging-related deterioration accumulating during the rest of
the entire adult life [1]. This idea of High Initial Damage Load (the
HIDL hypothesis) predicts that even a small progress in optimizing the
early-developmental processes can potentially result in a remarkable
prevention of many diseases in later life, postponement of
aging-related morbidity and mortality, and significant extension of
healthy lifespan [1-3]. Thus, the idea of early-life programming of
aging
and longevity may have important practical implications for developing
early-life interventions promoting health and longevity.
In this study
we tested the predictions of High Initial Damage Load (HIDL)
hypothesis. Specifically, the HIDL hypothesis predicts that early-life
events may affect survival in later adult life through the level of
initial damage. This prediction is confirmed for such early-life
factors as paternal age at person's conception [4] and the month of
person's birth [4,5].
Another testable prediction of the HIDL hypothesis is a prevision of an unusual non-linear pattern of lifespan inheritance. This prediction is tested and confirmed -- familial transmission of lifespan from parents to children follows a non-linear (accelerating) pattern with steeper slopes for offspring lifespan of longer-lived parents, as predicted [6].
An introductory section presented
earlier is written as an abstract briefly summarizing the main ideas,
findings and conclusions of our studies. The purpose of this section
is to provide a more detailed discussion of the idea of high initial
damage load.
Reliability theory of aging predicts
that a failure rate
of simple redundant systems increases with age according to the Weibull
(power) law [1-3]. This theoretical prediction is consistent with
empirical observations that failure kinetics of technical devices
follows the Weibull law [7]. However, biological systems 'prefer' to
fail
according to the Gompertz (exponential) law [1,8], which calls for
explanations.
An attempt to explain exponential
deterioration of
biosystems in terms of the reliability theory led us to a paradoxical
conjecture that biological systems start their adult life with high
load of initial damage [1-3].
Although this idea may look like a
counter-intuitive assumption, it fits well with many empirical
observations on massive cell losses in early development. For example,
the female human fetus at age 4-5 months possesses 6-7 million eggs
(oocytes). By birth, this number drops to 1-2 million and declines even
further. At the start of puberty in normal girls, there are only
0.3-0.5 million eggs - just only 4-8% of initial numbers (see review
[3]).
Massive cell losses in early
development are creating conditions for
Poisson distribution of organisms according to the numbers of remaining
cells, which in turn produce the exponential (Gompertzian) law of
mortality increase [1]. Because the mathematical proof for this
statement
is already published elsewhere for a more general case of binomial
distribution [1], we can concentrate here on substantive discussion of
the
idea of high initial damage load in biological systems.
Biological
systems are different from technical devices in two aspects. The first
fundamental feature of biosystems is that, in contrast to technical
(artificial) devices which are constructed out of previously
manufactured and tested components, organisms form themselves in
ontogenesis through a process of self-assembly out of de novo forming
and externally untested elements (cells). The second property of
organisms is the extraordinary degree of miniaturization of their
components (the microscopic dimensions of cells, as well as the
molecular dimensions of information carriers like DNA and RNA),
permitting the creation of a huge redundancy in the number of elements.
Thus, we can expect that for living organisms, in distinction to many
technical (manufactured) devices, the reliability of the system is
achieved not by the high initial quality of all the elements but by
their huge numbers (redundancy).
The fundamental difference in the
manner in which the system is formed (external assembly in the case of
technical devices and self-assembly in the case of biosystems) has two
important consequences. First, it leads to the macroscopicity of
technical devices in comparison with biosystems, since technical
devices are assembled 'top-down' with the participation of a
macroscopic system (man) and must be suitable for this macroscopic
system to use (i.e., commensurate with man). Organisms, on the other
hand, are assembled 'bottom-up' from molecules and cells, resulting in
an exceptionally high degree of miniaturization of the component parts.
Second, since technical devices are assembled under the control of man,
the opportunities to pretest components (external quality control) are
incomparably greater than in the self-assembly of biosystems. The
latter inevitably leads to organisms being 'littered' with a great
number of defective elements. As a result, the reliability of technical
devices is assured by the high quality of elements, with a strict limit
on their numbers because of size and cost limitations, while the
reliability of biosystems is assured by an exceptionally high degree of
redundancy to overcome the poor quality of some elements.
It follows from this concept of high initial damage load that even small progress in optimizing the processes of ontogenesis and increasing the numbers of initially functional elements can potentially result in a remarkable fall in mortality and a significant improvement in lifespan. This optimistic prediction is supported by experimental evidence of increased offspring lifespan in response to protection of parental germ cells against oxidative damage just by feeding the future parents with antioxidants [9]. Increased lifespan is also observed among the progeny of parents with a low resting respiration rate (proxy for the rate of oxidative damage to DNA of germ cells, see [1]. The concept of high initial damage load also predicts that early life events may affect survival in later adult life through the level of initial damage. This prediction proved to be correct for such early life indicators as parental age at a person's conception [4] and the month of person's birth (see table 1 and earlier publications [4,5]).
Women may be particularly sensitive to
early-life exposures, because they are mosaics of two different cell
types (one with an active paternal X chromosome and another one with an
active maternal X chromosome). The exact pattern of this mosaic is
determined early in life. If early-life conditions affect the
proportion (or distribution pattern) of cells with a given X
chromosome, such conditions might have long-lasting effects in later
life. Indeed, this conjecture of stronger female response to early-life
exposures is confirmed for such early-life predictors of adult life
span as paternal age at a person's conception [4] and the month of a
person's birth [4,5].
Another testable prediction of the HIDL
hypothesis
is a prediction of an unusual nonlinear pattern of life span
inheritance. Traditionally, it is assumed that the dependence of
progeny life span on parental life span should follow a linear
relationship, which is common to all other quantitative traits in
classic quantitative genetics [10]. In other words, for each additional
year of parental life span, the children are expected to have some
fixed gain in their average life span too, as a result of polygenic
inheritance of quantitative traits [10]. However, the HIDL hypothesis
leads to a very different prediction of a nonlinear (accelerated)
"concave-up" pattern of life span inheritance. There should be
virtually no life span heritability (a negligible response of progeny
life span to the changes in parental life span) when parental life span
is below a certain age, and a much higher heritability (an increased
response to parental life span) when parents live longer lives. This
prediction follows from the hypothesis of HIDL among short-lived
parents, whose bodies are damaged during early developmental processes,
although their germ cell DNA might be perfectly normal. (If the germ
cell DNA were damaged too, these short-lived parents would probably
produce offspring who also live short lives. This category will
therefore be unlikely to distort the linear dependence of offspring
life span on parental life span by a large amount.) Therefore, the
progeny of some short-lived parents may have quite normal life spans,
well beyond genetic expectations. This result would thus obstruct the
classic linear offspring-on-parent dependence for life span. Only at
some high parental life span, when most of the germ-normal/somatically
damaged parents are eliminated because of their shorter length of life,
will the classic linear pattern of life span inheritance eventually
reveal itself in its full capacity. This prediction of the HIDL
hypothesis was tested and confirmed in humans: Familial transmission of
life span from parents to children proved to follow a nonlinear
(accelerating) pattern, with steeper slopes for the life span of
offspring born to longer-lived parents, as predicted6.
Thus, there is mounting evidence now in support of the idea of fetal origins of adult degenerative diseases, and early-life programming of aging and longevity [4].
This study was made possible thanks to a generous support from the National Institute on Aging (NIH, USA), and a stimulating working environment at the Center on Aging, NORC/University of Chicago. We would like to thank members of the Science Advisory Board, SAB (http://www.scienceboard.net/) for useful comments on our work made at the SAB discussion group.
|
Month-of-birth |
Net effect*, |
Standard Error |
P value |
|
February |
0.00 |
Reference level |
|
|
March |
1.10 |
0.92 |
0.2331 |
|
April |
1.72 |
0.92 |
0.0619 |
|
May |
2.35 |
0.90 |
0.0090 |
|
June |
1.66 |
0.90 |
0.0665 |
|
July |
1.86 |
0.91 |
0.0404 |
|
August |
1.49 |
0.90 |
0.0978 |
|
September |
1.51 |
0.92 |
0.0986 |
|
October |
1.95 |
0.90 |
0.0308 |
|
November |
2.13 |
0.93 |
0.0229 |
|
December |
3.04 |
0.91 |
0.0009 |
|
January |
0.94 |
0.92 |
0.3086 |
|
February |
0.00 |
Reference level |
|
*Net effect corresponds to additional years of life gained (or lost) compared to the reference category (lifespan for those born in February).
Results for Table 1 are obtained through multivariate
regression analysis of lifespan data (outcome variable) for 6,908 women
born in 1800-1880 (extinct birth cohorts with lifespan known for each
person), who survived by age 30 (focus on analysis of adult lifespan).
The following additional predictor variables are also included in the
final model because of their predictive value: (1) calendar year of
birth, (2) ethnicity (Russian, British and others), (3) loss of father
during formative years of childhood (before age 15), (4) loss of mother
during formative years of childhood (before age 15), (5) cause of death
(violent vs non-violent), (6) early death of at least one sibling
(before age 30), (7) high birth order (7+), (8) nobility rank of the
father (indicator of social status), (9) large family size (number of
siblings 9+), (10) maternal lifespan, (11) paternal lifespan, (12)
paternal age at person's birth, (13) late paternal age at first
childbirth (50+ years), (14) birth of the first child by mother after
age 30, (15) death of mother from violent cause of death. The F-value
for regression model is 18.12 (p<0.0001).

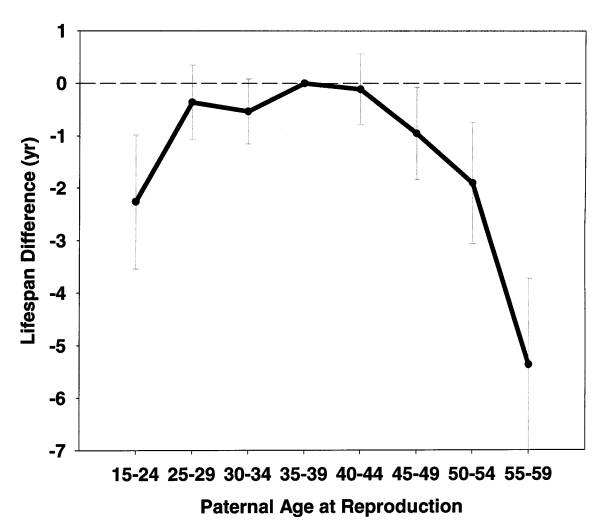
Figure 1. Daughters' lifespan as a function of paternal age at
daughter's birth. 5,063 daughters from European aristocratic families
born in 1800-1880. Both parents lived 50+ years. Details of data
analysis are described elsewhere [4].