Discussant: Leonid A. Gavrilov
Center on Aging, NORC and the University of Chicago
This is an interesting study, which suggests and applies new rigorous statistical methods to test the validity of the Gompertz law at extreme old ages. The author also suggested an explanation why the Gompertz law fails at older ages, based on the idea of population heterogeneity.
It is important to discuss the scientific background related to this study because the significance of this work could be more fully appreciated in the context of previous findings.
The current situation with applicability of the Gompertz law to
extreme
old ages is paradoxical. On the one hand, it is well known for a long
time
that the Gompertz law is not applicable to mortality rates at advanced
ages -- the observed mortality rates are always lower than predicted by
the Gompertz model, and, not surprisingly, the actual numbers of
survivors
to extreme ages is always higher than predicted by the Gompertz
law.
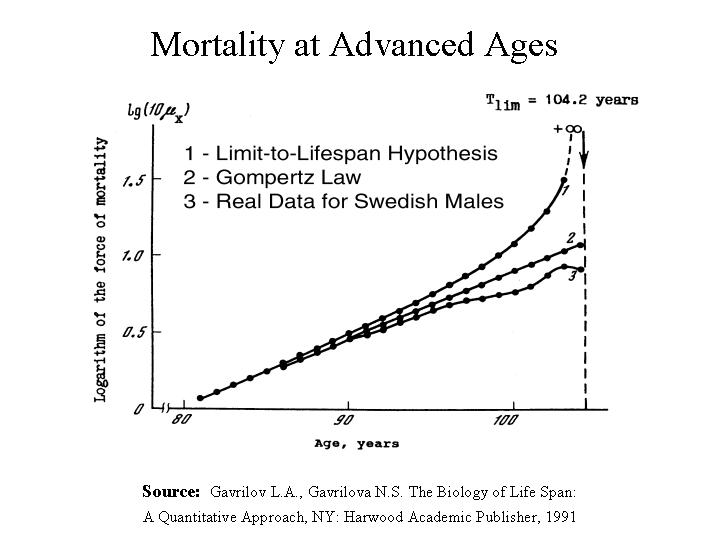
The picture below illustrates the mortality deceleration observed at
advanced
ages contrary to the predictions of the Gompertz law:

The scientific literature on the deviation of mortality rates from the Gompertz law at advanced ages is abundant, starting with the study of Benjamin Gompertz himself (Gompertz,1825; Makeham, 1867; Brownlee, 1919; Perks, 1932; Greenwood & Irwin, 1939; Mildvan & Strehler, 1960; Strehler, 1960; Economos, 1979,1980,1983,1985; Gavrilov & Gavrilova, 1991). The most recent and detailed review of the scientific literature on this issue was made by Olshansky (1998).
Paradoxically, the Gompertz law and the Gompertz-Makeham law are nevertheless often applied to estimate the oldest-old mortality rates by extrapolation in order to "close" the life tables. When confronted with the question why these "wrong" formulas are used, the demographers/actuaries usually reply that this is not an important issue, because life expectancy at birth is not very sensitive to the way how exactly the life tables are closed. The same "wrong" formulas and related assumptions are often used for graduation (smoothing procedures) of the mortality trajectories at advanced ages. It is extremely important, therefore, to know exactly how a particular life table was closed and/or graduated, before using it for testing of any statistical models. If the Gompertz or the Gompertz-Makeham laws were already introduced into the data by the method of life table construction/graduation, these data would not be useful for statistical hypothesis testing.
To summarize the coverage of scientific background, we may conclude that the Gompertz law is known to be not applicable to the oldest-old mortality, unless the data are spoiled by artificial introduction of this law during extrapolation/graduation procedures. The discussed study by Jack Yue confirms that the Gompertz law is indeed not applicable to the oldest-old mortality, and this conclusion validates the new statistical methods suggested by the author for testing the Gompertz law.
The next important question is: why is the Gompertz law not applicable to the oldest-old mortality? The author of the discussed paper suggests that this may be the result of population heterogeneity at advanced ages. The same hypothesis was also suggested by other authors (Carnes, Olshansky, 2001). There is, however, one problem with testing this hypothesis. It may be not difficult to generate the mortality trajectories that will be close to the observed trajectories by assuming that population is a mixture of subgroups of people with different Gompertz parameters. The real problem here is whether there is any sense in such computational exercise. Is there any direct evidence indicating increased population heterogeneity at advanced ages?
The answer to this question is provided at the picture below. The
graph
illustrates the dependence of daughters’ lifespan (expressed as
additional
years of life gained/lost compared to the reference lifespan level in
the
same birth cohort) as a function of maternal lifespan. For more on
methodological
details of this study see (Gavrilova, Gavrilov, 2001).
Interestingly
the dependence of daughters lifespan on maternal lifespan looks like
consisting
of two lines – one for shorter-lived mothers (died before age 85) with
very weak dependence of daughter's lifespan on maternal lifespan and
another
– for longer-lived mothers (died after age 85) with extremely strong
and
steep dependence.
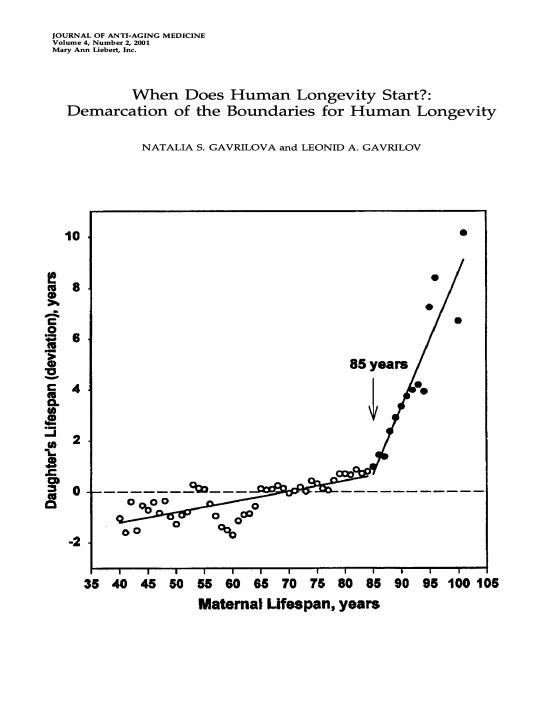
Daughters born to long-lived mothers may live 10 years longer on average if their mother reached age 100. This indicates that long-lived people are fundamentally different from other people in the sense that their children also live significantly longer lives. The breaking point at about age 85 for mothers indicates the age when deaths becomes much more selective in their timing and when population heterogeneity becomes an important issue.
Overall, the discussed paper contains interesting ideas and
important
findings on the oldest-old mortality, which correspond nicely with
results
obtained by other authors.
References
Brownlee, J. (1919) Notes on the biology of a life-table. J. Roy. Stat. Soc. 82, 34-77.
Carnes, B.A., Olshansky S.J. (2001) Heterogeneity and its biodemographic implications for longevity and mortality. Exp Gerontol. 36(3):419-30.
Economos, A.C. (1979) A non-gompertzian paradigm for mortality kinetics of metazoan animals and failure kinetics of manufactured products. AGE 2, 74-76.
Economos, A.C. (1980) Kinetics of metazoan mortality. J. Social Biol. Struct. 3, 317-329.
Economos, A.C. (1983) Rate of aging, rate of dying and the mechanism of mortality. Arch. Gerontol. and Geriatrics 1, 3-27.
Economos, A. (1985) Rate of aging, rate of dying and non-Gompertzian mortality - encore… Gerontology 31, 106-111.
Gavrilov, L.A., Gavrilova N.S. (1991) The Biology of Life Span: A Quantitative Approach, NY: Harwood Academic Publisher, 1991, 385p.
Gavrilov, L.A., Gavrilova N.S. (2001) The reliability theory of aging and longevity. Journal of Theoretical Biology, 213(4): 527-545.
Gavrilova, N.S., Gavrilov, L.A. (2001) When does human longevity start?: Demarcation of the boundaries for human longevity. Journal of Anti-Aging Medicine, 4(2): 115-124.
Greenwood, M. & Irwin, J.O. (1939) The biostatistics of senility. Hum. Biol. 11, 1-23.
Gompertz, B. (1825) On the nature of the function expressive of the law of human mortality and on a new mode of determining life contingencies. Philos. Trans. Roy. Soc. London A 115, 513-585.
Makeham, W.M. (1867) On the law of mortality. J. Inst. Actuaries 13, 325-358.
Mildvan, A. & Strehler, B.L. (1960) A critique of theories of mortality. In: The Biology of Aging (Strehler, B.L., Ebert, J.D., Glass, H.B., & Shock, N.W., eds), pp.216-235. Washington, D.C.: American Institute of Biological Sciences.
Olshansky, S.J. (1998) On the biodemography of aging: a review essay. Population and Development Review 24, 381-393.
Perks, W. (1932) On some experiments in the graduation of mortality statistics. J. Inst. Actuaries 63, 12-57.
Strehler, B.L. (1960) Fluctuating energy demands as determinants of
the death process (A parsimonious theory of the Gompertz function). In:
The
Biology of Aging (Strehler, B.L., Ebert, J.D., Glass, H.B., &
Shock,
N.W., eds), pp.309-314. Washington, D.C.: American Institute of
Biological
Sciences.
Contact address of the discussant:
Dr. Leonid A. Gavrilov, Center on Aging
NORC/University of Chicago
1155 East 60th Street
Chicago, IL 60637-2745
USA
Fax: (773) 256-6313, Phone: (773) 256-6359
FOR MORE INFO PLEASE VISIT OUR SCIENTIFIC WEBSITE :
http://longevity-science.org/